
Of all the equations in meteorology, the equation I will go over in this writing is my favorite! It is the Clausius-Clapeyron equation which relates saturation vapor pressure to the temperature. Vapor pressure is the pressure exerted by water vapor alone in millibars. As the amount of moisture increases, the vapor pressure increases. You may have heard a phrase such as “warm air can have more moisture than cold air”. This is the equation that shows the amount of moisture in the air for a given temperature. Below are the meanings of the symbols in the equation. Two versions of the equation are shown on the diagram below and I will go over each of these versions next. LN(Es/6.11) = (L/Rv )*(1/273 - 1/T) or LN(e/6.11) = (L/Rv )*(1/273 - 1/Td) Es / e = Saturation vapor pressure (in millibars) / vapor pressure (in millibars) L = Latent heat of vaporization = 2.453 × 10^6 J/kg Rv = Gas constant for moist air = 461 J/(kg*K) T / Td = Temperature in Kelvins / Dewpoint in Kelvins There are two version of the Clausius-Clapeyron equation and one relates the vapor pressure to the dewpoint and the other relates the saturation vapor pressure to the temperature. The equation to use in order to determine how much moisture is in the air outside is to use the equation that relates vapor pressure to the dewpoint. The other version of the equation is used to determine what could be the maximum amount of moisture in the air for a given temperature. Note both versions of the equation are equivalent when the relative humidity is 100%. If the air is unsaturated, then use the dewpoint to determine the amount of moisture in the air. 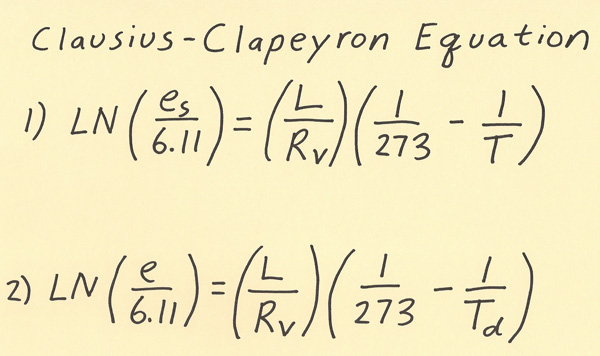 Here are a couple of example problems with working the Clausius-Clapeyron equation. 1) What is the vapor pressure when the dewpoint is 50.00 F? First convert Fahrenheit to Celsius (50.00 F = 10.00 C). Next, convert the Celsius temperature to Kelvins (10.00 C = 273.15 = 283.15 K). Next, insert into formula and solve algebraically. The algebra has several steps that are shown below: LN(e/6.11) = (L/Rv )*(1/273 - 1/Td) *plug in for Td: LN(e/6.11) = (L/Rv )*(1/273 - 1/283.15) *calculate value for (1/273 - 1/283.15) = (1/273 - 1/283.15) = 0.000131307 *calculate value for (L/Rv ) = 5,321.041215 *right side of equation is 5,321.041215 * 0.000131307 = 0.698689959 *advice: do not round off answers in intermediate steps, only round the final answer when problem is complete *equation is now: LN(e/6.11) = 0.698689959 *take exponent of each side: e/6.11 = e^0.698689959 = 2.011116336 *multiple both sides by 6.11: e = 12.28792081 mb, round final answer to 12.29 mb 2) What is the dewpoint when the vapor pressure is 12.29 mb? This is the same problem as #1 except it requires working backwards. I’m showing this problem so you can see the steps of working a problem if given vapor pressure and dewpoint needs to be found. LN(e/6.11) = (L/Rv )*(1/273 - 1/Td) *plug in for vapor pressure: LN(12.29/6.11) = (L/Rv )*(1/273 - 1/Td) *solve left side of equation using LN function of calculator: LN(12.29/6.11) = 0.69885915 *equation is now: 0.69885915 = (L/Rv )*(1/273 - 1/Td) *Solve for L/Rv and plug in: 0.69885915 = (5,321.041215)*(1/273 - 1/Td) *divide both sides by 5,321.041215 to get: 0.000131339 = (1/273 - 1/Td) *write 1/272 as a decimal and subtract this from both sides of equation *results in: -0.003531665 = - 1/Td *rearrange equation algebraically to get: Td = -1/-0.003531665 = 283.15 K = 10.00 C |